
Charles Greely Abbot
As we slowly climb out of the current steep sunspot minimum, it is worth reflecting upon some long-standing questions about our neighboring star. Over the long haul, is its output constant? Could it be a variable star? You can imagine the ultimate consequences to our planet if the flux of the giant radiator in our solar system that keeps us warm (and alive) is periodic or unstable (beyond the cycle of sunspots and a few other less pronounced (and less understood) fluctuations). Those questions followed naturally from an earlier mystery, first teed up for the scientific community at the end of the 19th century, of how hot the sun is – what is its temperature? Once that could be known and measured, scientists could determine its overall energy output and see if that value remains steady over time. Easier said than done, though. The following story is an example of the grit, determination, and incredible perseverance needed to pin down the value of single elusive number: the so-called solar constant.
From attempts to ascertain the true value of precession discovered by Hipparchus in the Hellenistic era to the Hubble constant in our own time, nailing down fundamental physical values and constants has been a necessary, ever-present preoccupation of science. The story of the hunt for the solar constant takes us into the trenches of science and to the far ends of the earth; it is an example of how science was done by the intrepid pioneers, and how it is still is done today in some fields. It’s also a window into the early days of astrophysics, when scientists were starting to appreciate the immense trove of information that could be gleaned from the careful study of spectra.
If I asked you to tell me how you would measure the temperature of the sun, what would you say? We’d agree the task is not too easy (at least before the era of earth satellites). If you said, “Let’s measure the sun’s energy output at various wavelengths and at various altitudes above the earth.” I’d say, that’s a good start, but then what? And you, astutely, would respond, “We’d then need to quantify the effects of atmospheric absorption (or, conversely, atmospheric transmission) at those wavelengths and altitudes.” Right again. And from that information you can use mathematics as a kind of telescope – extrapolating the data to estimate the value of those coefficients completely above the atmosphere. That would give you the value of solar energy arriving at the earth above its atmosphere, and free of atmospheric effects. And that’s the thing we’re looking for, the solar constant: the mean value of the solar radiation reaching Earth. (Readers who are purists will have noted immediately that something that has a ‘mean value’ is hardly a true physical constant (e.g., in the sense that the Newtonian gravitational constant, Planck’s constant, or Stephan-Boltzmann constant are constants); for now we’ll note your well-taken objections and move on.)
We could stop there, but the story gets even more interesting from that point on. This is because once the solar constant is in hand, we can mathematically shake out a host of other vital properties relating to our sun. By using the simple geometry of the sphere, we may estimate the value of the solar constant at the sun’s surface. From that emerges a value for the luminosity of the sun. From that, in turn, and a little help from the Stefan-Boltzmann relationship between radiation and temperature, we can calculate the temperature of the sun. Charles Greeley Abbot, the main hero of our story, amazingly came up with the solar temperature which is only slightly larger than the modern value.
We could continue down this solar rabbit-hole of inquiry. Once all that information is known, we can work back toward the earth again and calculate how warm the earth at its distance from the sun should theoretically be, as a so-called ideal or blackbody radiator. We could then compare the result with how warm it actually is, surrounded by its warming blanket of atmosphere. At that point we have some interesting insights as to why the earth’s surface is the temperature it happens to be, why the chemical composition of the atmosphere is so crucial to that temperature, and why the earth is at a ‘Goldilocks’ distance from the sun. But we’re getting way ahead of ourselves. Let’s begin our short story.
The Challenge
The Paris Academy of Sciences in 1876 offered a prize to the person who could solve one of the foremost problems of the day: to determine the temperature of the Sun. Earlier efforts had led to wildly disparate results, from a few thousands of degrees to tens of millions of degrees. John Herschel in 1837 had taken the first steps to measure the thermal output of the Sun at the Cape of Good Hope. He used a device he called an “actinometer” to measure the heat gain caused by the Sun in a known quantity of substance in a given time. At about the same time, Claude Pouillet of France was engaged in the same purpose, using a similar device called by him a “pyrheliometer.” He found that the Sun’s rays on each square centimeter of the Earth’s surface would raise the temperature of a gram of water by 1.7633 degrees C in one minute. This number he called the “solar constant.” The unit of heat is the “calorie.” This data yields information about the amount of the Sun’s radiant energy reaching the Earth. To take this information and deduce the actual solar constant – that is, independent of the effects of the atmosphere – was, however, not so easy. Unknown was the amount by which the Earth’s atmosphere intercepts the Sun’s radiation. The ignorance of the amount of atmospheric shielding of solar radiation would lead to misleadingly low values at the Earth’s surface for the Sun’s actual output.
Langley’s Bolometer and the Sun’s Infrared Spectrum
A fundamentally important development in getting an empirical measurement of the Sun’s energy production was the invention by Samuel P. Langley (1834 – 1906) of the bolometer. Langley, a creative visionary who would later become famous for his early experiments in aviation, became director of Allegheny Observatory in western Pennsylvania, and then went to the Smithsonian Institution in Washington, where he was instrumental in founding the Smithsonian Astrophysical Observatory, becoming its first director.

Samuel Langley
Langley’s ingenious bolometer was a breakthrough invention. By means of the small changes induced in the electrical conduction of a strip of platinum, the bolometer could measure the radiant energy received from the Sun in regions never before mapped, and well outside of the visible spectrum. It was so sensitive that he could move its detector along the trace of the spectrum of the Sun produced by a diffraction grating and measure the relative intensities of radiation at each wavelength. From this he could determine the solar constant in a new way: by measuring the Sun’s received radiation wavelength by wavelength, as the bolometer was moved across the image of the Sun’s spectrum, and then summing up the results. With the bolometer he discovered that the solar spectrum cuts off sharply in the ultraviolet but stretches many octaves (to use historian of astronomy Agnes Clerk’s phrase) into the infrared. This meant that the visible radiation heretofore known and measured by the eye of man was only a fraction of the amount streaming down upon the Earth, mostly in the form of heat.
These were completely new findings. His research eliminated the former distinctions between light and heat. The belief that heat and light were distinct was held by Sir William Herschel and deemed gospel since the early 1800’s. As you’ll remember from your high school physics class, though (if you were paying attention), they are not distinct: they are merely radiation of different wavelengths. Langley’s bolometer revealed the continuity of solar radiation to at least 5.3 microns (or 5,300 nanometers – billionths of a meter, abbreviated by the Greek letter mu) into the infrared, and its uneven receipt at the surface of the Earth, where infrared radiation was admitted by gaps and holes the atmospheric screen, and also where it was obstructed. Beyond 5.3µ the radiation was too feeble for detection by Langley’s instruments (though modern instruments have carried this much farther). These measurements into the new infrared realm were a huge improvement over the limits of the visible range of radiation, which is between about 400 and 700 nm (.4µ and .7µ). They opened the door to a new study of the infrared spectrum of the Sun.
The Effects of Atmospheric Absorption
Any measurements of the solar spectrum and calculation of the solar constant must take into account many factors, among them the true distance between the Earth and Sun when the measurements are made (since the Earth’s orbit is elliptical) and must above all correct for the absorption of the Sun’s radiation at each wavelength by the heavy blanket of Earth’s the atmosphere. The solar constant is in fact defined for Earth’s mean distance to the Sun (one astronomical unit), as if the measurements were made completely above the Earth’s atmosphere. Only this would give a true picture of the Sun’s radiative output reaching Earth. Since at that time there were no artificial satellites to measure the Sun’s radiation above the atmosphere, Langley had to do something else to determine the coefficient of transmission of the atmosphere at each wavelength. He organized an expedition to fourteen-thousand-foot Mt. Whitney, in the Sierra Nevada mountains in California. Using his bolometer, he recorded the radiation received at selective wavelengths at various times of the day. Since he knew the angle of the Sun from the zenith (zenith angle) at the time of each observation, he could compute the relative length of the air mass through which the rays of the Sun traveled at each wavelength. By this means, Langley in 1881 was able to make the first estimates of the amount of radiation transmitted from the Sun at each wavelength through our atmosphere. The intensity of radiation at each wavelength (measured by the galvanometer deflections from his bolometer) multiplied by the coefficient of transmission for each wavelength, and summed over the whole spectral range, would (after application of certain instrumental and other corrections) yield the total solar energy received as if the instrument were outside the Earth’s atmosphere. This would have to be compared with pyrheliometer readings to find the correspondence between intensity of radiation and calories.
Langley found the solar constant at the Earth’s surface to be 1.36 calories per minute per square meter. (The solar constant today is usually stated in terms of watts per square meter; we’ll talk later about modern values.) Correcting for the effects of atmospheric absorption, he derived a (incorrect) solar constant of 2.54. Thus, he found that overall not even sixty percent of the Sun’s radiation is transmitted by the atmosphere. This understated the transmission of the atmosphere. His work was pioneering, and he acknowledged that his determination of the solar constant was “provisional” and would need to be refined with repeated thorough observations. It led others into the field, some of whom derived constants as high as 3 and even 4. These were well off the mark. Langley’s graph of the solar spectrum and his corrected curve above it, from his March, 1903 article in the Astrophysical Journal article, The Solar Constant and Related Problems, is shown below.
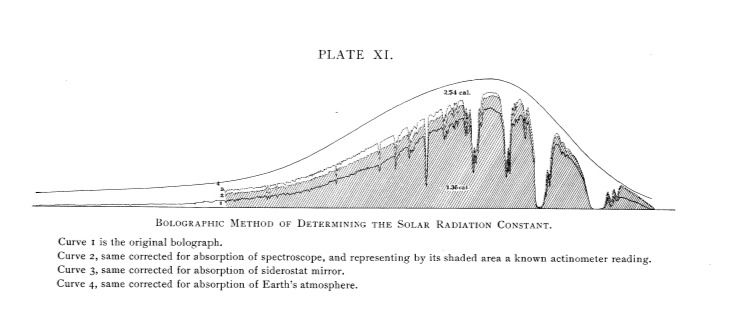
The lower curve shows what his instruments received, and a correction for instrumental error, and the uppermost, smoothed curve shows the inferred solar constant, after the effects of atmospheric absorption had been taken into account. His paper in the Astrophysical Journal with the historic ‘bolograph’ may be found at http://articles.adsabs.harvard.edu//full/1903ApJ....17...89L/0000090.000.html.
Enter Charles Greeley Abbot
After Langley’s death, his assistant, Charles Greely Abbot (1872 – 1973), the real hero of our story, succeeded Langley as director of SAO in 1907 and later as secretary of the Smithsonian Institution. Abbot continued and refined Langley’s work with great diligence. He organized expeditions to Mt. Wilson and Mt. Whitney from 1905 to 1910, and to Bassour, Algeria, and in 1914 took a balloon 24 kilometers above the Earth. (Imagine, riding in a balloon over Algeria in 1914!) Early on, Abbot realized something was wrong with Langley’s result, that he had evidently miscalculated the coefficients of transmission. Abbot’s work up to about 1906 led him to deduce a solar constant of 2.01, later revised by him downward to a value of 1.93, which is somewhat closer to the modern value of 1.95. We’ll get into Abbot’s work more in the next part of the story.
Comments