Newton, Halley, and the “Prodigious Comet of the Year 1680”
- Douglas MacDougal
- Jul 23, 2024
- 14 min read

A surprising celestial event may have ripple effects on the progress of science. It can be a catalyst for reexamination of old paradigms, inspire new lines of investigation, or even help confirm a theory. This is about a spectacular heavenly appearance toward the end of the 17th century that had all of those consequences.
One of the unresolved outliers in Isaac Newton’s Principia and his theory of gravitation was what to do about comets. Book III of his Principia, which Newton described as “the most difficult of the whole book,” recounts his difficulties in applying his laws of gravitation – so brilliantly demonstrated with the moons and planets of the solar system – to the motion comets. Part of the trouble lay with overcoming a longstanding assumption of how comets moved through space. Another had to do with the extreme nature of certain comets. They are rarely seen to move circularly like planets or their moons. Traditionally associated with terrifying omens [1], the most dramatic comets will enter the solar system at breakneck speeds in kamikaze dives toward the sun, some almost hitting it, creating brief, glorious, tailed spectacles in the sky for all to wonder at, depict, write about, and remember, then vanish into the void as quickly as they came.
Though comets have held us earthlings in thrall for centuries, the real dawn of cometary astronomy may have begun with the appearance of an unpretentious smudge of light seen telescopically in the morning sky over Germany, evidence of a visitor that would soon have an important and inspiring impact on the history of science.
Discovery
Gottfried Kirch of Saxony was an astronomer who made his living by publishing calendars and ephemerides. Despite having fourteen children (or perhaps because of it), Kirch found time to look at celestial objects through his telescope. On the morning of November 4th, 1680, as Kirch was surveilling the crescent moon and Mars, he swept up a “sort of nebulous spot, of an uncommon appearance” in the constellation of Leo. It showed no tail. Two days later, it had shifted position and now sported a short tail: telltale signs that Gottfried Kirch had discovered a comet [2].
And what a comet it was! One of the great comets of the seventeenth century, Kirch’s comet became (sadly for his naming rights) “The Great Comet of 1680,” and later, “Newton’s Comet.” It put on a spectacular show around the world, becoming one of the rare comets visible even in daylight. It was a morning showpiece, with a 20- or 30-degree tail, brightening through November and early December as it neared the sun. By early December however, it had disappeared in the sun’s glare. We will call this morning visitor, now gone from sight, Comet 1.
On December 20th, another glorious spectacle appeared in the western evening sky. Early Dutch settlers in New York stated that “there appeared an extraordinary comet, it caused very great consternation throughout the province.” Some watchers attributed a golden hue to its tail, making it all the more beautiful. The comet presented a dazzling spectacle to earthlings on December evenings. Its tail was said to have reached 70° in length, even 90⁰ by some reports from Europe. It remained visible to the naked eye until February 1681. Issac Newton followed it telescopically until mid-March 1681. We’ll call this Comet 2.
One comet or two?
This double celestial spectacle afforded the opportunity for a historic and fruitful mathematical collaboration between Isaac Newton and Edmund Halley. Newton, the brilliant loner famous for his prickly defensiveness would not be at the top of one’s list of warm, affable collaborators. Yet Halley was different; their mutual respect ran deep, and their long relationship was “warm and happy” [3]. (The greatly gifted Halley would soon devote three years of his life to getting Newton’s Principia edited and published [4].) The main challenge for Newton was to apply his newly minted laws of motion to ascertain the object’s orbital parameters.
But first a question: could these cometary apparitions be two separate bodies that flirted by us in late 1680? Or were they one and the same? It was hard to say they must be the same. Comet 1, though beautiful, was less dramatic than show-stopper Comet 2. Its tail was shorter and otherwise not obviously a twin to the other. According to NASA/JPL research scientist Donald K. Yeomans, “The November comet was a morning object with a relatively modest tail, while the one in December was a bright evening object with an enormous tail. Not only did they appear physically dissimilar, but their apparent motions, when taken together, could not be represented with any figure resembling a circle or a straight line” [5].
To understand the confusion, we must recall that Newton, and everybody else at the time, thought that comets moved rectilinearly across the sky. That they traversed the solar system on straight-line paths as they approached or passed by the sun. Once seen, a comet would fly out of the solar system as fast as it came in, never to return. As a purely transient object, there would thus be no possibility of predicting its reappearance [6]. Halley later noted how Kepler and Hevelius thought interloping comets moved rectilinearly, or nearly so, although calculations didn’t quite square with that assumption [7]. In any event, when Comet 1 was seen in the morning sky headed toward the sun, later followed by Comet 2 sailing away from the sun, Newton assumed he had observed two different comets [8].
Newton thought they were two, John Flamsteed (1646-1719) thought they were one. Flamsteed, the first Astronomer Royal, was an observer not a theorist. In one of the first of many disputes with Newton that would later reach epic proportions, he argued in letters that some kind of “magnetic attraction” moved the body around the sun, returning it in the same direction that it had appeared. Newton summarily disposed of Flamsteed’ s magnetic argument and asserted that the observed motions seemed too paradoxical to fix a single body: “its motion was thrice accelerated and retarded” [9].
While Newton was trying to work out the path of the Great Comet of 1680, be it two or one, another heavenly visitor appeared in 1682. Newton’s observations of this comet – known to us now as Halley’s Comet – together with new data on both comets from a childhood friend in Maryland, helped turn his mind. They convinced him that rectilinear paths simply could not work as a mathematical template of cometary motion. Indeed, unpublished manuscripts from around that time show Newton trying to compute a trajectory for the 1680 comet from four observations. But it was not until September 1685 that he confessed in a letter to Flamsteed that the Astronomer Royal was right: “taking that of 1680 into fresh consideration, it seems very probable that those of November and December were ye same comet” [10].
Halley looks at history
The comet’s timing coincided with Newton’s work on the laws of motion, and his Book III of the Principia contains pages of recorded observations, data, analyses, and drawings. Both Newton and Halley had recognized that this well-observed (and measured) comet would be a good further test of Newton’s laws of motion. In Halley’s words, written some years later:
At length, came that prodigious Comet of the Year 1680, which descending (as it were) from an infinite Distance Perpendicularly towards the Sun, arose from him again with as great a Velocity. This Comet, (which was seen for Four Months continually) by the very remarkable and peculiar Curvity of its Orbit (above all others) gave the fittest Occasion for investigating the Theory of the Motion [11].
Using a subset of observations gathered by Flamsteed, himself, and others, Newton, “partly by arithmetical operations, and partly by scale and compass” plotted the path of the comet. He then assessed his findings against other observations in his set of data to see if his orbit fit those, which it only roughly did. Halley then “determined the orbit to a greater accuracy by an arithmetical calculus than could be done by graphic operations,” and significantly reduced the fitting errors in longitude and latitude. The question remained whether the Comet of 1680 was a one-time visitor on a parabolic track, or bound by the sun’s gravity in an elliptical orbit, and therefore destined to return. It was a question of mathematical fine tuning that even today requires exceptionally accurate observations.
Halley put forth an argument from historical records that the Comet of 1680 was the same object that people had seen at least twice before, with repeat visits every 575 years. Here is how Newton described Halley’s insight in his Book III of the Principia:
Moreover, Dr. Halley, observing that a remarkable comet had appeared four times at equal intervals of 575 years (that is, in the month of September after Julius Caesar was killed; An. Chr. 531, in the consulate of Lampadius and Orestes; An. Chr. 1106, in the month of February; and at the end of the year 1680; and that with a long and remarkable tail, except when it was seen at Caesar’s death, at which time, by reason of the inconvenient situation of the earth, the tail was not so conspicuous), set himself to find out an elliptic orbit whose greater axis should be 1382957 parts, the mean distance of the earth from the sun containing 10000 such; in this orbit a comet might revolve in 575 years . . . [and with] the equal time of perihelion Dec. 7d. 23h. 9m. . . and its conjugate axis 18481.2, he computed the motions of the comet in this elliptic orbit [12].
With his calculations and this information, Newton concluded that the orbit of Comet of 1680 was not parabolic, but was in a high-eccentricity elliptical orbit [13]. Here from Book III of the Principia is the first depiction in history of a comet path rounding the sun:
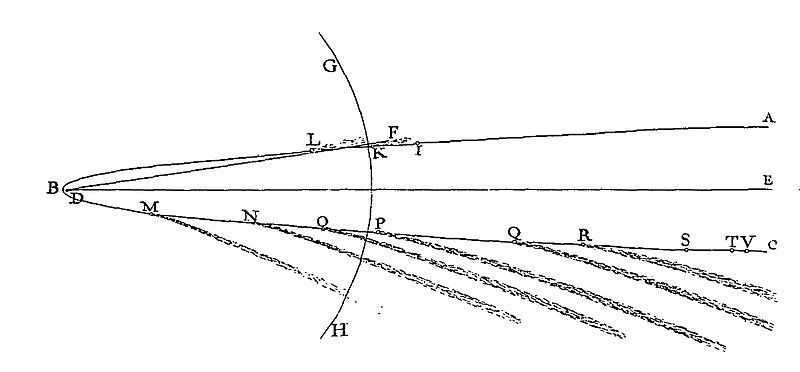
The key difference between a first approximation of a parabolic orbit and the ultimate resolution in favor of an elliptical orbit seems to have been the existence of a long historical record that Halley found to suggest it [14]. It was also a dramatic early demonstration of how difficult it can be to distinguish among any of three types of orbits (elliptical, parabolic and hyperbolic) in that fine zone just slightly this side or the other of eccentricity one [15]. In truth, though, finding matching returns of 575 years in the historical record should not have led Halley and Newton to conclude that the comets of 531, 1106, and 1680 were one and the same comet. While the first two ancient visitors made dramatic shows and were spaced as Halley noted, their full orbital parameters of were unknown, so their common identity with the Comet of 1680 couldn’t be confirmed [16]. But the idea was certainly in the air, at least, that when comet elements are known, one can indeed make intelligent comparisons in history and predict future returns, as Halley was soon to do brilliantly with the Comet of 1682.
With Halley’s help and much calculation, Isaac Newton cracked the comet problem and finished his Book III as one of the most elegant treatises-within-a-treatise in scientific history. By encompassing comets within his mathematical model of celestial motion, he demonstrated that they are just other members of the solar system, smaller than most, but subject to the same mathematical laws that govern the rest of the solar menagerie. It began a productive cottage industry of comet observation and analysis throughout the following century.
Halley wrote the first review of the Principia in the Royal Society’s Philosophical Transactions. It was succinct and glowing. About the mathematical conquest of the orbit of the Comet of 1680, he said:
Lastly the Theory of the Motion of Comets is attempted with such success, that in an example of the great Comet which appeared in 1680/1681, the Motion thereof is computed as exactly as we can pretend to give the places of the primary Planets; and a general Method is here laid down to state and determine the Trajectory of Comets, by an easy Geometrical Construction; upon supposition that those Curves are Parabolic, or so near it that the Parabola may serve without sensible Error; tho’ it be more probable, saith our Author, that these Orbs are Elliptical, and that after long periods Comets may return again [17].
During this period too, polymath Halley busied himself on many other scientific tasks, among them compiling a synopsis of all comets in the historical record for which he could obtain data to compute their orbital elements [18]. His grand synthesis appeared in 1705 under the title A Synopsis of the Astronomy of Comets. It showed, among other things, striking similarities of the elements of the comets of 1531, 1607, and 1682. From detecting close similarities in their orbital elements, he was able to conclude that these sightings were of one and the same comet in an elliptical orbit. He famously predicted its return in 1758: Hence I dare venture to foretell that it will return again in the year 1758. And, if it should then return, we shall have no reason to doubt but the rest must return too [19]. Though Halley died in 1742 at age 85, his comet reappeared, almost miraculously it seemed at the time, on Christmas Day in 1758, and Halley’s name became forever attached to it [20].
A certifiably prodigious comet
Halley’s Comet comes back reliably in each generation because its orbit is safely not hair-pin elliptical and never allows the comet to get too riskily close to the sun. The Great Comet of 1680, on the other hand, was a hell-raiser, a daredevil of a comet, trading safety for show by venturing scorchingly close to the solar furnace. To see what this means, let us look at a few of its elements.
The Comet of 1680 was inclined about sixty degrees from the ecliptic plane. The semi-major axis (the long axis of the ellipse, symbol a) of the ellipse, from Newton’s data was 69.14785 AU (astronomical units). Based on Newton’s measurements, we can also calculate the eccentricity of the comet’s orbit to have been about .9999107 which is very close to one, which suggests a nearly parabolic orbit. Its aphelion distance (farthest distance from the sun, called Q) from the Principia data works out to 138.3 AU. Its perihelion distance (closest distance to the sun, called q) is the eye-popping figure of note: at .006 AU, this was an extremely close perihelion, one of the closest ever [21]. It was less than a million kilometers from the center of the sun, whose mean radius is about 697,000 kilometers. It grazed the solar surface at an altitude of only about 227,000 kilometers. My mathematical simulation of the sun’s globe and the comet’s path curving about a third of the solar radius off its surface gives a hint of it.

We can also calculate that the comet’s velocity at perihelion was about 535 kilometers per second as it zoomed low over the sun’s surface. It’s hard to grasp this. If we scale it to earth, so that the earth is the sun’s size, we’d have to imagine such an object streaking 2,000 kilometers high across our earth’s sky (about 1,200 miles up) – at GPS satellite altitude (medium earth orbit) – going 1.2 million miles per hour! Its remarkably close encounter with the Sun explains why the comet was so astonishingly brilliant when it reappeared in December to begin its return home.
More modern analyses have refined these numbers. The NASA/JPL website [22] shows the applicable elements to be e = .999986, a = 444.4285714 (i.e., a much larger semi-major axis than Newton had figured) and q = .006222. The inner-orbit plot and perihelion velocity of this comet are virtually the same as Newton's original; yet with these modifications, where we are so close to parabolic, its takes only the smallest tweak to make truly enormous differences in the semimajor axis distance and period of revolution. Here, with the major axis Q of over 888 AU, the period becomes almost 9,400 years [23]!
NOTES
The picture at the top of this article is of the Comet of 1680, painted by Lambert Doomer in January, 1681. Rijksmuseum Description: Night landscape with the large comet (tail star) seen on a field outside the Geesterpoort in Alkmaar in January 1681. It is part of the Rijksmuseum collection in the public domain. http://hdl.handle.net/10934/RM0001.COLLECT.36825
[1] “When beggars die, there are no comets seen; The heavens themselves blaze forth the death of princes.” Shakespeare, Julius Caesar, Act II, Scene 2.
[2] The comet that Kirch discovered was the first discovered through the lens of a telescope.
[3] See “Halley and the Principia” by Robert E Schofield, in Isaac Newton’s Papers & Letters on Natural Philosophy, 397 et seq., edited by I. Bernard Cohen (Cambridge: Harvard University Press, 1958) (hereafter Halley and the Principia).
[4] Gjertsen, Derek. The Newton Handbook, 249 (London: Routledge & Kegan Paul, 1986) (hereafter referred to as The Newton Handbook).
[5] Yeomans, Donald K. Comets: A Chronological History of Observation, Science, Math, and Folklore, 96 (New York: John Wiley & Sons, Inc., 1991) (hereafter referred to as Comets). Dr. Yeomans, now retired, was a research scientist at NASA/JPL and is a near-Earth object specialist.
[6] The Newton Handbook 125.
[7] See Halley, Edmund, A Synopsis of the Astronomy of Comets, 10-11 (London: 1705) (hereafter referred to as Halley’s Synopsis). See also Bartusiak, Archives of The Universe, n. 20 below, for the relevant selected text of Halley’s Synopsis. Here is the full text of the section in question from page 21 of Halley’s Synopsis:
“This great Astronomer [Kepler] had the Opportunity of observing Two Comets, one of which was a very remarkable one. And from the Observations of these (which afforded sufficient indications of an annual parallax) he concluded that the Comets moved freely through the Planetary Orbs, with a Motion not much different from a Rectilinear one; but of what Kind, he could not then precisely determine. Next, Hevelius (a Noble Emulator of Tycho Brahe) following in Kepler’s Steps, embraced the same Hypothesis of the Rectilinear Motion of Comets, himself accurately observing many of them. Yet, he complained, that his Calculations did not perfectly agree to the Matter of Fact in the Heavens: And was aware, that the Path of a Comet was bent into a Curve Line towards the Sun.”
[8] This and the following narrative about Flamsteed and Newton’s change of mind are drawn from The Newton Handbook 125.
[9] These conclusions stemmed from misunderstandings in the data communicated from Flamsteed, including the use of two different calendar systems, which were eventually sorted out.
[10] The Newton Handbook 126.
[11] Halley’s Synopsis 5. The spelling of words from this and other early sources in this article has been updated to a more modern style, but capitalization and italics are as in the original.
[12] Principia, Book III, Prop. XLI, p. 515.
[13] The “greater axis” and “conjugate axis” in the description are the respective major and minor axes of the ellipse. The semi-major axis a and semi-minor axis b are half those. Since an astronomical unit is the mean distance between the Earth and Sun, Newton’s phrase, “the mean distance of the earth from the sun containing 10000 such . . .” means that given distances are in ten-thousandths of an astronomical unit. So, to convert to AU, the data must be divided by 10,000. With the units in hand being AU and years, we can easily check its period with Kepler’s Third Law and compute the other elements. See, e.g., Douglas MacDougal, Newton’s Gravity: An Introductory Guide to the Mechanics of the Universe, 281-286 (New York: Springer, 2012), where I’ve worked through the math on this example.
[14] This same approach led Halley famously to conclude that the comet of 1682 was also periodic, with the predicted return time of 75 years, which prediction was confirmed after his death; as a tribute to that great man, that comet became known as Halley’s Comet. See generally, Halley’s Synopsis.
It has been argued that Edmond Halley was ahead of his time in appreciating the importance of history in scientific research, that “he developed a more thorough-going historical awareness than did most of his recent scientific predecessors or contemporaries.” Chapman, Alan. “Edmond Halley’s Use of Historical Evidence in the Advancement of Science.” Notes Rec. R. Soc. Lond. 48 (July 1994):167–191. http://doi.org/10.1098/rsnr.1994.0022.
[15] Eccentricities where e < 1 are ellipses; e = 1 are parabolas; e >1 are hyperbolas. Newton stated in one corollary that comet orbits “will be so near to parabolas, that parabolas may be used for them without sensible error.” Principia, Book III, Prop. XL, Cor. 2.
[16] Comets, 122. Yeomans believes the attribution to be incorrect. Without comparison of each one’s orbital elements, elements that were not available for such early apparitions, it is fruitless to match comets on the basis of just period and appearance.
[17] Halley and the Principia 410.
[18] Halley explained the purpose of his Synopsis: “The principal life therefore of this Table of the Elements of their Motions, and that which induced me to construct it, is, That whenever a new Comet shall appear, we may be able to know, by comparing together the Elements, whether it be any of those which has appeared before, and consequently to determine its Period, and the axis of its Orbit, and to foretell its Return. And, indeed, there are many Things which make me believe that the Comet which Apian observed in the Year 1531 was the same with that which Kepler and Longomontanus took Notice of and described in the Year 1607 and which I myself have seen return, and observed in the Year 1682.” Halley’s Synopsis 21.
[19] Halley’s Synopsis 22.
[20] The event made an enormous impact. In the words of science historian Marcia Bartusiak, “The public was bedazzled and Newton’s clinics were instantly silenced. It was at that moment that Newton’s controversial law of gravity was at last triumphant among both scientists and the public, and Halley’s name became forever linked to the periodic celestial visitor.” Marcia Bartusiak, Archives of The Universe: A Treasury of Astronomy's Historical Works of Discovery, 100 (York: Pantheon books, 2004).
[21] One of the closest ever, but C/2011 W3 (Lovejoy) was a sungrazer that was closer by a hair. Its slightly greater eccentricity was .9999294, and its perihelion distance q was .0055538 AU.
[22] See http://ssd.jpl.nasa.gov/sbdb.cgi#top . The Great Comet of 1680 is designated C/1680 V1.
[23] When e = 1 the closed elliptical curve has snapped open and the comet will not return. This orbit is exceedingly close to that point!
Comments